数独スコアラーAndroid版公開
【C#】消えたクリップボード
VisualStudio2017を2019に更新して軽いプログラムを作ろうとしたらクリップボードクラスが見つかりません。
おっと参照マネージャーでPresentationCoreDLLを追加しないとダメだったな
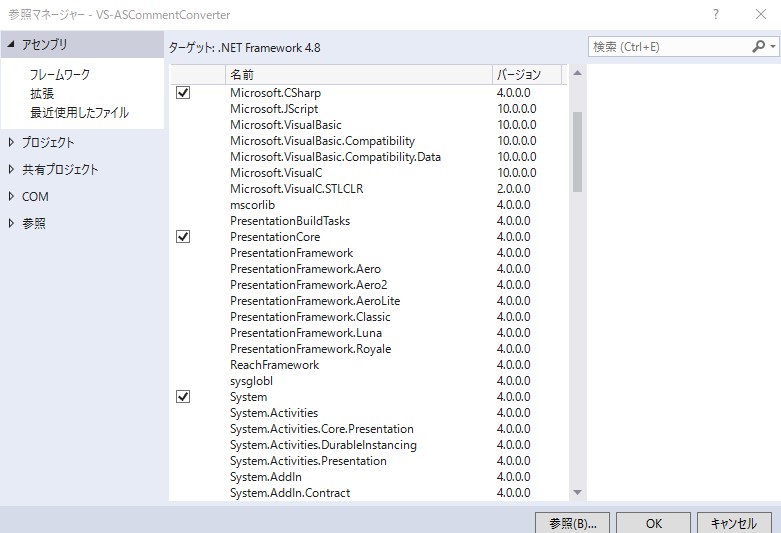
あれっ、参照がないぞ?こういう感じで表示されてるはずなのに

というか参照ってこんなんだったっけ?ツリーも違くない?
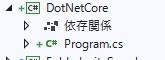
で、最初のプロジェクト作成に戻ってみるとフレームワークが.NetCore(OS非依存のやつ)になってました。
以前は一番上に.NetFrameworkがあったので流れで押してしまったらしい。

どうもCoreでクリップボードクラスは実装されていないようです。
stackoverrun.com
というわけで.NetFrameworkプロジェクトで作り直したら無事クリップボードクラスが使えました。


【Java】関数ポインタ的なもの
複数の関数を一つの配列にして任意の順番で実行するために関数ポインタ的なものが欲しくなりました。
C#だとDelegateでしたが、Javaだと関数型インターフェースがそれにあたるようです。
関数型インターフェースは抽象メソッドを1つだけ持つインターフェースで、任意の関数を渡してからその抽象メソッドを実行すると、渡した関数が実行されます。
関数型インターフェースは自分で定義してもいいのですが、引数の数や戻り値の種類ごとにデフォルトでいくつか用意されているので、通常はそれで事足りるでしょう。
今回はint型二次元配列arr1、arr2を2つ渡したかったので、BiConsumerを配列にして使います。
そこへ以下のようにSolverというクラスの4つの関数ShareCandidateLogic、PairLogic、CrossLogic、TripleLogicを突っ込みました。
Solver solver = new Solver(); BiConsumer<int[][],int[][]>[] logics = new BiConsumer[4]; logics[0] = solver::ShareCandidateLogic; logics[1] = solver::PairLogic; logics[2] = solver::CrossLogic; logics[3] = solver::TripleLogic; logics[3].accept(arr1, arr2); logics[1].accept(arr1, arr2); logics[0].accept(arr1, arr2); logics[2].accept(arr1, arr2); logics[2].accept(arr1, arr2); logics[3].accept(arr1, arr2); logics[0].accept(arr1, arr2); logics[1].accept(arr1, arr2);
関数を参照するときにはクラス参照のピリオドを::に変えます。
BiConsumerではacceptメソッドが定義されているので、これを実行すると中身の関数に引数が渡された状態で実行されます。
【Java】C#からLINQを移植したら結構違った
C#からjavaに移植しようとしたときにLINQはどうするのかと思ったらstreamというものがあるんですね。
記法が若干違う(Whereがfilterとか)ぐらいで同じように使えるかと思ったら仕様がだいぶ違ったのでメモ。
C#のコード List<int> intList = new List<int>(); intList.Add(1); intList.Add(2); intList.Add(3); if (intList.Where(s => s >= 2).Count() > 0) { string str=""; intList.Where(s => s >= 2).Select(s => str += s.ToString()); }
リスト内に2以上の数字があったならそれらを文字列に変換してstrにつなげる処理です。
上記を実行しようとするとエラーだらけになりました。
主なエラーは3つ。
エラー1:記法が違う
ラムダ式はC#では=>ですが、javaでは->です。
Whereはfilter、Selectはmapになります。
C#だとListからLINQが使えますが、Javaはstreamを生成する必要があります。
エラー2:ラムダ式内で変数は処理できない。
ラムダ式の中でfinal変数以外を処理できないようです。以下のエラーが出ます。
Variable used in lambda expression should be final or effectively final
エラー3:streamが途中で止まる
java.lang.IllegalStateException: stream has already been operated upon or closed
ググってみるとstreamは終端処理(countとかtoArrayとか)をしてしまうとそれ以上処理ができなくなるようです。
countの時点でstreamが閉じているので再度生成しないといけません。
上記を踏まえて修正すると以下のようなコードになりました。
List<Integer> intList = new ArrayList<Integer>(); intList.add(1); intList.add(2); intList.add(3); Stream<Integer> repetitionStream = intList.stream().filter(s -> s >= 2); if (repetitionStream.count() > 0) { String str = ""; repetitionStream = intList.stream().filter(s -> s >= 2); Integer[] arr = repetitionStream.toArray(Integer[]::new); for (Integer k : arr) str += k.toString(); Log.d("result",str); }
countの後で再度streamを生成しています。
ラムダ式内で変数処理ができないので拡張for文を使ってSelect処理の代わりをやってます。